SGU-401-450

 2021/12/19 

450 Ramen Shop

题意

分析模拟。

449 Dendrograms

题意（画树状图）

分析按 Y 值从大到小合并并查集。

448 Controlled Tournament

题意有个选手参与锦标赛，已知每对选手之间对阵的比赛结果，求冠军是的方案数。

分析状压 DP。

447 Optimal Rest

题意 Rest command 使用字符 'R' 和一个停留时长表示，其中停留时长，'1' 表示停 1 拍，'2' 表示停半拍，'4' 表示停 1/4 拍，以此类推。字符 '.' 表示当前停留时长是前一个停留时长的一半，比如 R1. 表示先停 1 拍，然后再停半拍。最短停留时长不能少于 1/64 拍。给一长度为的 rest command 合法序列将其转化成表达式最短的序列，若有多个解则输出字典序最小的表达式。

分析从样例可以看出，两个表达式的总停留时长是一致的，而合法的表达式是有限的，因此可以转换成背包问题。

446 Rotation Estimation

题意使用个二维平面点表示星座图，给出前后拍摄得到的星座图上各点坐标，求星座图最小旋转角度。

分析将两张星座图的中心点平移至原点，然后挑第一张图的任意一点，在第二章图找到相匹配的点。匹配原理借助极角排序即可。

445 Dig or Climb

题意 Red 按照路线图从走到，路线图是一条折线，折线上的点分别为，速度为。Red 也可以重新开辟点到点的捷径，其速度为。求从起点到终点的最小花费时间，其中。

分析 dp。

444 Headstrong Student

题意给定两个正整数，求的循环部分长度。

分析模拟。

443 Everlasting...?

题意定义 key number 为一个正整数的最大质因子减去其它质因子的和。给定两个数，判断哪个数的 key number 更大（数据保证两个数的 key number 不同）。

分析

442 X+R(X)=N

题意给一个大数，求有多少个满足，其中表示的数位翻转，如。

分析：

假设，表示第个位置是否有进位，且。
显然有，。进位受的影响，受的影响。
由外向内处理时，仅需考虑相邻位的进位即可，自然而然地使用：表示区间的两个端点，表示位置是否产生进位，表示位置是否借位，同理。状态可转移到。

441 Set Division

题意将个不同的物品放入个相同的盒子种，求方案数对 2007 取模。

分析第二类斯特林数。

440 Moles and Holes

题意给二维平面上个点，若个点 A, B, C 构成的锐角 A 满足等于的第 3 位小数，记为一个合法的三元组。求合法三元组的所有数量。

分析

参考青少年信息学奥林匹克竞赛-Sgu440解题报告

439 A Secret Book

题意给长度分别为和两个字符串，先求出第二个字符串的最小表示，然后循环移位第一个字符串，使得转换后的第一个字符串开头与第二个字符串匹配或仅一个字符不同。题目保证存在解，求第一个字符串的最小移动次数，其中。

分析扩展 KMP。

438 The Glorious Karlutka River =)

题意有个人要从河的一岸跳到河的另一岸。河中有个石头，每个石头的坐标为，每个石头最多同时容纳个人。每个人跳远的最远的距离是，每次跳跃需花费 1 秒钟。求所有人都跳到河对岸的最少花费时间或判断不可能。

分析：

如果有解，答案不超过。因为如果存在通路，第二个及以后的人顺着第一个人的路径走即可。
按时间分层建模网络流，当流量总和达到时便是最小时间花费。

437 Hexodoku

完整题面 https://www.eolymp.com/en/contests/3632/problems/29681

题意将数字填入下图中的格子中，要求：1）相邻格子的数字不同；2）每“行”的数字均不相同；3 ）以黑色格子为中心的 7 个格子组成一个 cell，cell 中的数字均不相同。已知某些格子已经填数，求字典序排名第个序列。

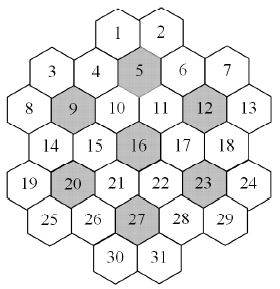
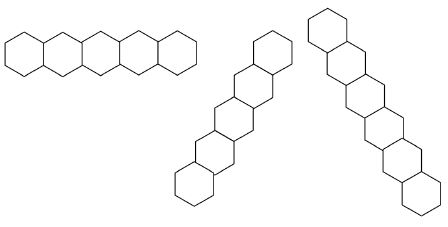
分析（？DLX 搜索）

436 The Diputs notation

题意

分析模拟（maybe）。

435 UFO Circles

题意给个圆，所有数字绝对值不超过 1000。求被覆盖奇数次的面积和覆盖偶数次的面积。

分析：

圆的离散化模板题。按照以及圆的交点纵坐标划分圆，相邻纵坐标构成的区间将圆划分成圆弧和梯形，基于这两种形状计算面积。
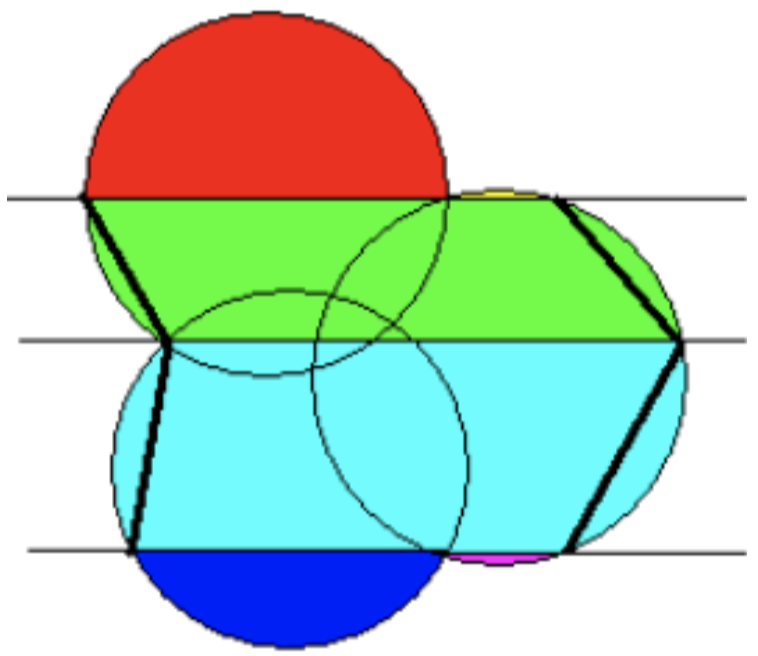
相邻纵坐标构成的区间中，每个区间包含若干左圆弧和右圆弧，可以视为合法的括号序列。根据这一性质，可以计算当前形状的覆盖次数。

参考 sgu 435 UFO Circles

434 Chemists

题意有个容器，每个容器当前有升液体。每次操作从一个容器中倒出任意多的液体到另一个容器中，使得第个容器最终有升液体，求最少的操作次数或判断不可行。

分析：

假设有个容器以及个容器，如果，那么至多需要次操作。对于液体有多余的个容器，每个容器需倾倒到其他的容器中，承接的容器中必然有一个容器仍没有达到目的（如果达到目的，说明可以将这个集合划分成两个新集合以减少操作次数），那就需要额外一次操作。
记表示集合状态为能创建最多的集合数，每次转移需枚举子集满足，则时间复杂度为。
当从一个的状态转移到一个状态时，就可以创建一个新集合，而不需关心具体的集合状态，时间复杂度可以降至。

433 Japhshan and Ramshut

题意有种砖头，第种砖头的形状是的长条。现使用这些砖头铺满大小的网格图，求任一方案或判断不可行。

分析状态压缩+动态规划。每次使用一种砖头覆盖坐标最小且未被覆盖的格子。需要注意的事，横向覆盖和纵向覆盖的二进制表示需要预处理，时间复杂度为。

432 XYZX 2009

题意（字符串模拟题）

分析模拟。

431 Wildcards

题意使用小写字母, 和匹配个字符串，并且不能匹配给定个字符串，求任一匹配方案或判断无解，其中可以匹配任意子串（包括空串），匹配任意小写字母。数据保证每个字符串长度不超过 11。

分析

430 Unit-distance graph

题意给个点的图，要求在二维平面给每个点设定坐标使得有连边的点在平面图上的距离为 1，没有连边的点的距离不为 1，输出任一方案。

分析

429 Problem Stacks

题意有堆石子排成一排，每堆石子有个。两个人轮流从第一堆或最后一堆石子取任意数量的石子，取走最后一个石子的玩家获胜。要求判断先手胜还是后手胜。

分析

当时，显然先手胜。
当时，问题就是普通的取石子游戏，判断异或和即可。具体操作：当两堆石子数量一致时，后手复制先手的操作就能取走最后一个石子。
当时，分情况讨论
- 若前两堆石子或后两堆石子数量相同时，先手必胜（将问题转化成的情形）。
- 若前两堆和后两堆石子数量不同，若第一堆和最后一堆石子不相同，先手可以操作使得第一堆和最后一堆石子数量相同，之后复制对手除取光石堆以外的操作。当对手取光一堆石子后，先手可以立即让剩余两堆数量一样。
当时，
当时，

428 Rebus

题意

定义 proper addition rebus 为，使用大写字母表示数字使得形如 ABC+CBA=BDB 的加法等式成立。
要求加数与加数的和位数相同；该形式下有且仅有一组解，即字母与数字之间有且仅有一种映射；字母之间的置换视为相同的解。
输出 1000 个 proper addition rebus，每个等式的长度不超过 100。

分析

因为加数和加数的和位数相同，即没有最高位进位。
RRR+TTR=EDT 符合条件，那么 RRRTTR+TTRRRR=EDTEDT 也符合条件。

427 Hamiltonian polyhedron

题意

分析

426 Double cyclic

题意给一个个元素的序列，其元素为。通过循环位移得到字典序最小的序列记为最小循环位移。给定常数，分别求序列的最小循环位移序列的第个元素。

分析

425 Control function

题意给大小的矩形，要求找到一个值域在的函数满足，即第一行与其他行不相同。数据保证。

分析：

对于第 2 行至第行，每行与第一行不同的列有很多，如果考虑选择哪一列作为 diff 项显然是很复杂的。
假设每一行任选一列，将数字视为点，diff 列连边，构建一张新的无向图。原问题转化成，使用对新图进行染色，要求相邻点的颜色不相同。
对于个点的全连接图，需要种颜色染色，才能保证相邻点的颜色不同。而新的无向图边数是，即使用不超过 51 种颜色即可对新的无向图进行染色。

424 Beautiful graph

题意使用不超过个点构造不包含自环的无向图，使得没有任意两个简单环有且仅有一条共同边，要求边数最多。

分析

423 Battle

题意

分析（贪心？）

422 Fast Typing

题意 Vasya 使用键盘输入个字符，第个字符输错的概率为。Vasya 检查输入正确性需要花费秒。当 Vasya 发现错误时，会按退格键回退到正确的字符前然后重新输入。输入字符和退格键均花费 1 秒。求 Vasya 正确输入个字符的最小期望时间。

分析表示输入前个字符的最小期望时间。

421 k-th Product

题意给个整数，从中取个数的乘积第大值。

分析

参考 https://blog.sengxian.com/solutions/bzoj-1425

420 Number Permutations

题意两个正整数定义为相似时，当且仅当两个正整数的十进制位数相同，并能通过排列数位相互转换，如 123 和 213 是相似的。求区间中有且仅有 1 个相似数字的数的个数。

分析枚举数位的最小排列，那么情况有种，直接计算即可。

419 Hexagonal Walkaround

题意在六边形网格上从起点方向走向终点方向为最少需要几个回合。每个回合允许向当前方向前进 1 格或者逆时针旋转 60 度方向后前进 1 格。不允许在一个方向上连续前进格。

分析

418 Deducing Grammar

题意

分析

417 Heavy Disc

题意给圆心半径为的圆，保证原点不在圆内。已知圆内一点处的密度为，求整个圆的质量。

分析

416 Optimal Dartboard

题意将填入双层飞镖靶上，如下图所示。要求相邻格子上的数的方差之和最大，更具体地，。

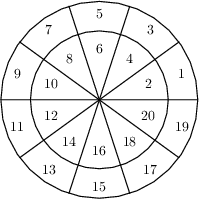
分析（构造）

415 Necessary Coins

题意有枚硬币，第枚硬币价值元。现需支付元，判断哪些硬币必然会用于支付。

分析

表示使用前枚硬币支付元是否可行。前向和后向分别动态规划，在去除第枚硬币后看前后硬币是否能支付元即可判断该枚硬币是否必须。
使用 bitset 优化：前向 dp 时从 0 开始记录，后向 dp 则从 xxxx 开始记录，则时间复杂度由降至。

414 Orthogonal Circles

题意给二维平面上个圆，求一个圆使得该圆和给定的所有圆都正交。两个圆正交，当且仅当两圆有交点且在交点的切线相互垂直。

分析记所求圆的圆心坐标以及半径为。因为圆的切线与切点-圆心垂直，则相交圆的切线过圆心，两个圆心与切点构成直角三角形。联立多个三角形即可求解 3 个变量。

413 Berland Division

题意给 2 ≤ n ≤ 100 个点，1 ≤ m ≤ 1000 条边的无向图（保证 n 是偶数，且不存在重边和自环），要求划分点集，满足：每个子集大小不少于 2；每个子集中的点对之间有且仅有一条路径，即导出子图是一棵树，输出任一划分方案。

分析使用 DFS 构树，那么兄弟节点没有边，继而有每个节点及其儿子节点都是一棵树的结论。但该做法在树根上可能出现根没有分组的情况，需分情况讨论：

尝试将根分配给某一儿子节点的分组中。
若无法直接分配，说明每个分组下都有一孙子节点和根有边相连。若该分组的点数大于 2，则重新将孙子节点和根分成一组即可。
剩余情况为：每个儿子节点的分组均只有 2 个点，根据奇偶性的性质，有一儿子节点所在的分组连接了一点数为奇数的子树（不考虑分组），将儿子节点或孙子节点分配给这棵子树得到偶数个节点的“新树”，则得到了原问题的子问题，递归求解即可。

参考：姜碧野 - SGU413 Berland Division 解题报告

412 Expedition

题意给个点的凸包，凸包内有条线段。坐标原点 (0,0) 处有一盏灯（数据保证原点在凸包内），部分凸包的边会被线段挡住光线，求被遮挡的凸包边的长度总和。

分析扫描线+极角排序。

411 Petya the Hero

题意给长度为 2000 的字符串，求最长公共子串。

分析二分+hash。

410 Galaxy in danger

题意有堆石子，第堆有个。有 2 种操作：从所有石子中都取走 1 个；将第堆石子的数量翻倍，即乘 2。求最少操作次数拿走所有石子。

分析贪心。假设单堆石子的最大数量为 A，其余堆石子在满足不超过 A 的前提下不断翻倍，数量记为 a，显然，否则可以继续翻倍。然后从所有石子中取走 1 个，直至，此时将翻倍后两堆石子数量便相同了。

409 Berland Flag

题意给的网格进行黑白染色，要求：1）每行恰好有个黑色格子；2）每列恰好有个黑色格子；3）每个子矩阵中恰好有个黑色格子。求出任一染色方案。

分析构造。构造任一满足条件的子矩阵，然后填充大矩阵中即可。

408 Game with points

题意从起点 (0, 0) 开始画个点，假设第步要画点，要求该点与相连成线段，要求：不在先前的线段上；距离不超过 1，且不与其他线段相交。每画完一点后，求当前有公共顶点的线段最大数量以及点对之间最大的欧几里得距离，两者相乘作为本次得分。求画完个点后的最大得分总和。

分析贪心。每次要么有公共顶点的线段最大数量 +1，要么点对的最大距离 +1，两值尽可能相同以使乘积尽可能大，最后形成类似蒲公英的形状。

407 Number of Paths in the Empire

题意有个城镇位于山脚下且形成一个环，每个城镇与相邻两个城镇有道路相连。首都位于山顶且与所有 n 个城镇相连。在可重复经过道路和城镇的前提下，求从首都出发经过条道路后回到首都的方案数。

分析动态规划。容易想到表示经过条道路后位于城镇的方案数。但注意山脚下的所有城镇本质上都是一样的，因此只需要区分首都和城镇，即表示在首都的方案数，表示在山脚城镇的方案数。

406 Goggle

题意数据库中有条序列，第条序列长，序列元素的值域是 [1, 100]。现有条查询，每次查询如 a,-b,c 形式，表示查询包含 a, c 且不包含 b 的序列。

分析 bitset。

405 Totalizator

题意观众竞猜两队比分结果，有 4 条得分规则（详见题面）。给定赛后两队的得分和个观众的猜测结果，求每位观众的得分。

分析模拟。

404 Fortune-telling with camomile

题意给长为的字符串列表，求第个位置的字符串。因为列表是循环的，所以存在的情况。

分析模拟。

403 Scientific Problem

题意给定整数，求数使得。

分析

402 Terrorists in Berland

题意给个点和条边的有权无向图，第条边的权重为。现要求破坏一个点以及若干条边，将原图划分成不连通的两部分，求最小边权和。

分析枚举删除点，剩下的交给全局最小割算法 Stoer-Wagner。

代码 402

401 Geologist Dubrovsky

题意： 有条南北走向的河流，第条河宽 , 流速为。主角在静止水流中游泳速度可达。判断主角能否在时间内从河流西岸游到东岸，若能则求出距离起点最远距离。

分析河流是南北走向，不影响主角东西走向的游泳速度。若到达对岸的时间有剩余，则贪心分配给纵向距离最远的河道。

原文作者：Mcginn

原文链接：http://mcginn7.github.io/2021/12/19/SGU-401-450/

发表日期：December 19th 2021, 5:17:27 pm

更新日期：May 4th 2024, 5:07:17 pm

Next Post

求解无向图最小割
Previous Post

SGU-351-400

CATALOG