斜率优化
针对形如：
的动态规划转移方程，可通过’’斜率’’的单调性进行优化。
题一、[HNOI2008]玩具装箱TOY
给定长为 $1\le N\le 50000$ 的序列 $1\le C_i\le 10^7$，将序列分成若干连续段，每段 $[i, j]$ 的花费为
其中 $L$ 为常数，$1\le L \le 10^7$。要求计算总的最小花费代价。
解题思路
利用前缀和 $S_i$，区间 $[i, j]$ 序列和可表示成 $S_j - S_{i-1}$。容易想到 dp 转移方程为：
将变量整理归类，记 $a_j=j+S_j, b_i=i+S_i+L+1$，则 $cost(i, j)$ 转化成：
转移方程移项可得：
因为 $a_j$ 在 $j$ 固定时可认为是个定值，故问题相当于最小化 $dp(j)-a_j^2$，进而可以将问题看成是斜率为 $2a_j$ 的直线，找出一点 $(b_i, dp(i)+b_i^2)$ 使得直线在 $y$ 轴的截距 $dp(j) - a_j^2$ 最小。
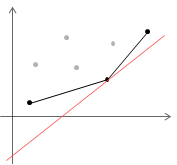图 1. 下凸壳。灰色点和黑色点分别表示非凸壳点和凸壳点。
显然，截距最小的关键点必然在下凸壳上，且下凸壳的每段斜率是单调递增的。
斜率为 $g$ 的直线截距最小所对应的最优点是，该点前一段斜率 $\lt g$，后一段斜率 $\gt g$。
注意 $1\le C_i \Rightarrow S_i \lt S_{i + 1} \Rightarrow a_i=i+S_i \lt a_{i + 1}=(i + 1) + S_{i + 1}$，斜率 $a_i$ 是单调递增的，则对应的最优点位置也是单调的，所以这种情况可通过双端队列将复杂度优化到 $O(n)$。
题二、小A与最大子段和
给定长为 $1\le N \le 2\times 10^5$ 的序列 $0 \le |A_i| \le 2000$，找一个非空连续子段 $B$，最大化：
解题思路
把问题进一步公式化：
为了去除 $\sum$ ，引入前缀和 $S_i$ 和 $V_i=\sum_{p=1}^i p\times A_p$，公式 (1) 转化成：
根据变量下标整理归类：
同”玩具装箱TOY”，此时相当于令截距 $Ans - V_j$ 最大，所以此时需要维护点集 $(i, iS_i-V_i)$ 的上凸壳。
因为 $A_i$ 存在负数，故斜率 $S_i$ 并不具有单调性，所以需要二分确定最优点的位置。
参考
斜率优化DP
斜率优化dp小结
代码
[HNOI2008]玩具装箱TOY
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| #include<bits/stdc++.h>
using namespace std;
typedef double db;
typedef long long ll;
typedef vector<int> vi;
typedef pair<int, int> pii;
#define fi first
#define se second
#define pb push_back
#define sz(x) ((int)(x).size())
#define all(x) begin(x),end(x)
#define rep(i,l,r) for(int i=(l);i<(r);++i)
#define per(i,l,r) for(int i=(r)-1;i>=(l);--i)
#define dd(x) cout << #x << "=" << x << ", "
#define de(x) cout << #x << "=" << x << endl
const int N = 5e5 + 7;
int n, L, C[N];
ll S[N], dp[N];
struct P {
ll x, y;
P() {}
P(ll _x, ll _y) {
x = _x, y = _y;
}
P operator-(const P &p) const {
return P(x - p.x, y - p.y);
}
ll operator^(const P &p) const {
return x * p.y - y * p.x;
}
};
#define X(i) (i + S[i] + L + 1)
#define Y(i) (dp[i] + X(i) * X(i))
int main() {
scanf("%d%d", &n, &L);
rep(i, 1, n + 1) scanf("%d", C + i);
rep(i, 1, n + 1) S[i] = S[i - 1] + C[i];
deque<P> Q; Q.push_back(P(X(0), Y(0)));
rep(i, 1, n + 1) {
ll g = 2 * (i + S[i]);
while (sz(Q) > 1 && (Q[1].y - Q[0].y) < (Q[1].x - Q[0].x) * g)
Q.pop_front();
dp[i] = Q[0].y - g * Q[0].x + (i + S[i]) * (i + S[i]);
P a(X(i), Y(i));
while (sz(Q) > 1 && ((Q[sz(Q) - 2] - a) ^ (Q.back() - a)) <= 0)
Q.pop_back();
Q.push_back(a);
}
printf("%lld", dp[n]);
return 0;
}
|
小A与最大子段和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
| #include<bits/stdc++.h>
using namespace std;
typedef double db;
typedef long long ll;
typedef vector<int> vi;
typedef pair<int, int> pii;
#define fi first
#define se second
#define pb push_back
#define sz(x) ((int)(x).size())
#define all(x) begin(x),end(x)
#define rep(i,l,r) for(int i=(l);i<(r);++i)
#define per(i,l,r) for(int i=(r)-1;i>=(l);--i)
#define dd(x) cout << #x << "=" << x << ", "
#define de(x) cout << #x << "=" << x << endl
const int N = 2e5 + 7;
int n, a[N];
ll S[N], V[N];
#define X(i) (i)
#define Y(i) (i * S[i] - V[i])
struct P {
ll x, y;
P() {} P(ll _x, ll _y) { x = _x, y = _y; }
P operator-(const P &p) const {
return P(x - p.x, y - p.y);
}
ll operator^(const P &p) const {
return x * p.y - y * p.x;
}
};
bool chk(deque<P> &Q, int i, ll G) {
return (Q[i + 1].y - Q[i].y) >= (Q[i + 1].x - Q[i].x) * G;
}
int main() {
scanf("%d", &n);
rep(i, 1, n + 1) scanf("%d", a + i);
rep(i, 1, n + 1) S[i] = S[i - 1] + a[i];
rep(i, 1, n + 1) V[i] = V[i - 1] + i * a[i];
deque<P> Q; Q.push_back(P(X(0), Y(0)));
ll ans = LLONG_MIN;
rep(i, 1, n + 1) {
int l = 0, r = max(0, sz(Q) - 2);
while (l + 1 < r) {
int z = (l + r) >> 1;
chk(Q, z, S[i]) ? l = z : r = z;
}
int j = l;
if (chk(Q, r, S[i])) j = r + 1;
else if (chk(Q, l, S[i])) j = l + 1;
else j = l;
ll f = Q[j].y - S[i] * Q[j].x + V[i];
ans = max(ans, f);
P a(X(i), Y(i));
while (sz(Q) > 1 && ((Q[sz(Q) - 2] - a) ^ (Q.back() - a)) >= 0)
Q.pop_back();
Q.push_back(a);
}
printf("%lld", ans);
return 0;
}
|
